高校数学Ⅱ
 5分でわかる!θ と θ+π、θ-πの関係
5分でわかる!θ と θ+π、θ-πの関係

- ポイント
- 例題
- 練習

この動画の要点まとめ
ポイント
θとθ+π,π-θの関係
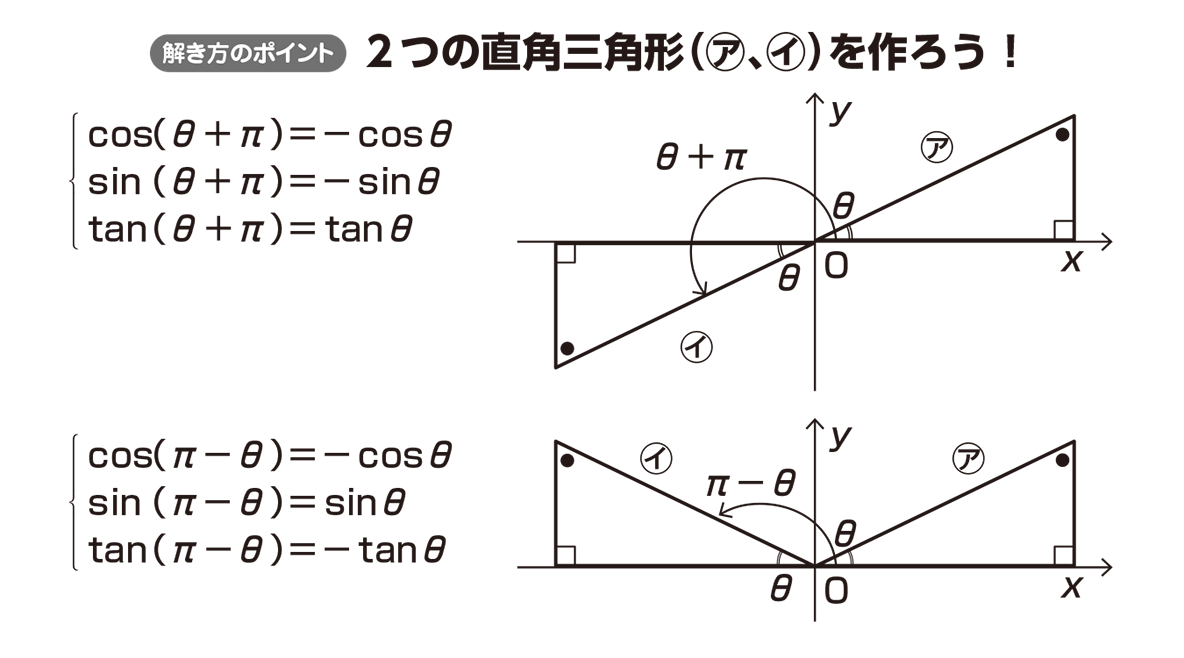
これでわかる!
ポイントの解説授業
θとθ+π,π-θの関係を覚えよう
POINT


公式を丸暗記するのではなく考え方を理解し、自分でも求められるようにしましょう。
π=180°を足すと、第1象限➔第3象限

角度がθの直角三角形を図に示し、θ+πがどの位置に移るのか考えてみましょう。
角度θの直角三角形アが第1象限にあったとします。θ+πということは、ここから更に π=180° 移動した場所に直角三角形が来ることを表しています。 第3象限 に移動してイの三角形になりますね。


このイの直角三角形に注目しましょう。

cos(θ+π)の値は 底辺/斜辺 で, アの直角三角形の底辺/斜辺と同じ になりますね。ただし、cosの符号は 第3象限でマイナス なので、 cos(θ+π)=-cosθ と表せます。

sin(θ+π)やtan(θ+π)も同様に考えると、ポイントのような公式が成り立ちます。

π=180°からθを引くと、第1象限➔第2象限

では、π-θも同じように考えてみましょう。
大事なのは 2つの三角形を書くこと です。
アの直角三角形を第1象限に書き、始線からπ移動してθ戻った場所すなわち π-θ の場所に三角形をとると、イの直角三角形は第2象限にとれますね。
これを使ってθ+πの時と同じように考えていきます。


このイの直角三角形に注目しましょう。

cos(π-θ)の値は 底辺/斜辺 で, アの直角三角形の底辺/斜辺と同じ になりますね。ただしcosの符号は 第2象限でマイナス なので、 cos(θ+π)=-cosθ と表せます。

sin(π-θ)やtan(π-θ)も同様に考えると、ポイントのような公式が成り立ちます。


公式を丸暗記しようと思うと大変です! 自分でしっかり求められるようにすることが大事です。







































今回のテーマは「θとθ+π,π-θの関係」です。
θ+π,π-θに関してはsin,cos,tanθの重要な公式があります。