高校数学Ⅱ
 5分でわかる!θ と θ+(π/2)の関係
5分でわかる!θ と θ+(π/2)の関係

- ポイント
- 例題
- 練習

この動画の要点まとめ
ポイント
θとθ+π/2の関係
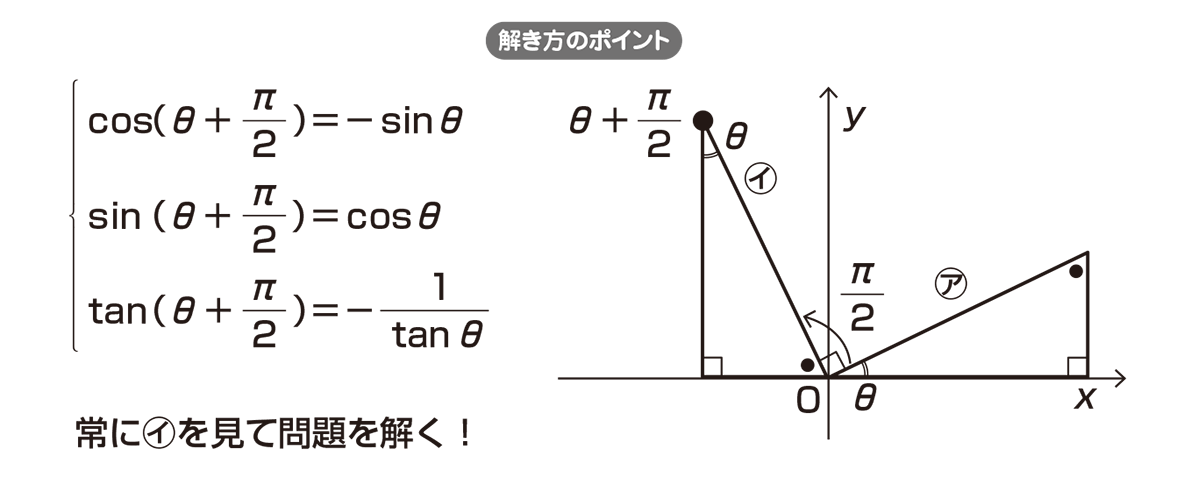
これでわかる!
ポイントの解説授業
θとθ+π/2の関係を見てみよう
POINT

「底辺」と「高さ」が入れ替わる!

角度θの直角三角形 が 第1象限 にあるときを考えます。
θ+π/2ということは、θから π/2 移動した場所に三角形が来ることを表しますね。
π/2=90° なので、直角三角形アは 第2象限 の直角三角形イに移動します。

ここで注意!
直角三角形イの右下にくる角度は、180°から(θ+π/2)を引いた角度なので90°-θになりますね。さらに直角三角形の上にくる角度はθになります。直角三角形アと直角三角形イでは、 底辺と高さが入れ替わります ね。

「cos」と「sin」が入れ替わる! 符号にも注意を!

では、直角三角形イで(θ+π/2)の三角比を考えましょう。

「底辺」と「高さ」が入れ替わっているので、
cos(θ+π/2)=-sinθ
sin(θ+π/2)=cosθ
tan(θ+π/2)=-1/tanθ
と表せます。
符号の変化にも注意してください。

では、ポイントを使って実際に問題を解いてみましょう。







































今回のテーマは「θとθ+π/2の関係」です。
前回学習したθ+π,π-θにくわえ、θ+π/2にもsin,cos,tanθの重要な公式があります。ポイントを確認しましょう。