単振動は等速円運動を横から見た運動のことです。では、 単振動する物体の位置 はどう表すことができるか考えてみましょう。

半径Aの円周上をまわる物体の等速円運動を例にします。次の図のように、円の中心を通る上下の直線をx軸として定めてみましょう。

物体には、日光のような平行線が右側からあたっているとイメージして下さい。すると、どうなるでしょうか。x軸には円運動の影が映りますね。時刻0[s]での物体の影の位置はちょうど、x軸の原点の位置に存在しているということがわかります。そして角θだけ進んだ時刻t[s]のときには、影の位置は◯で囲った位置まで移動します。つまり、t秒後の影の位置が単振動の位置そのものということになります。

では、時刻t[s]のときの物体の位置xを式で表していきましょう。時刻t[s]のときの物体から横軸に向かって垂線を降ろし、角θをもつ直角三角形をつくります。すると、この直角三角形の高さこそが単振動の位置ということになりますよね。

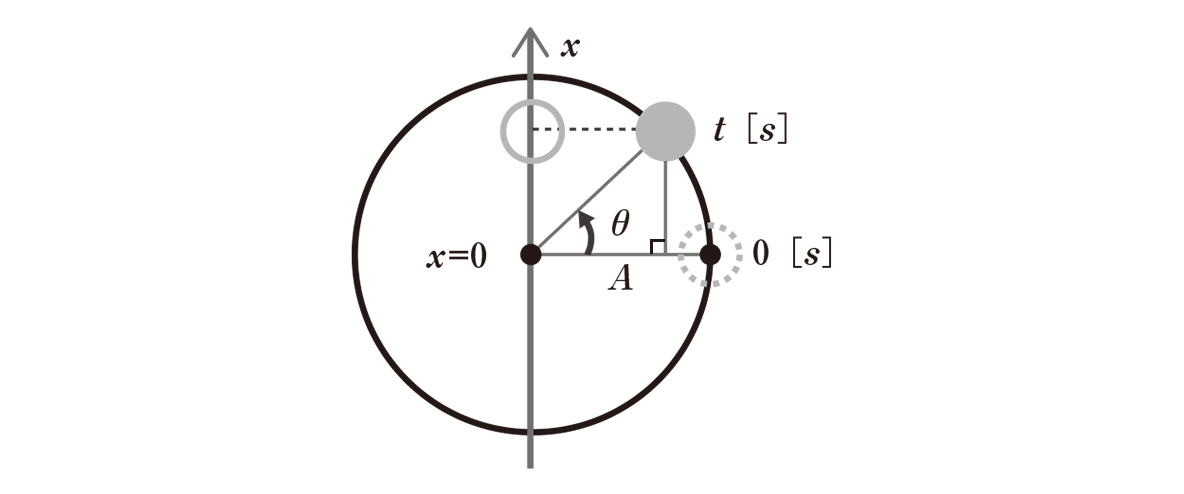
つまり、 単振動の物体の位置x は、
x=Asinθ
と表すことができるのです。

さらに、等速円運動の角速度をωとすると、ωは 1秒間に進む角度 のことなので、 θ=ωt と表せますね。したがって、 単振動の物体の位置x は、
x=Asinωt
と表すことができるのです。

Aは 単振動の振幅 と言います。ωのことを円運動では角速度と言いましたが、単振動でのωは 角振動数 と言います。さらにωtのことを 位相 と言います。数学ではこれを角度と言いますが、物理では位相ということを覚えてください。

単振動の位置x=Asinωtの式から、x-tグラフを作成してみましょう。三角関数sinのグラフは、原点から始まる周期的な曲線を描きます。

物体が1周するのにかかる時間が周期Tです。x-tグラフでは、最高点まで上がったあとに、最下点まで下がり、またx=0に戻ると時刻T[s]になります。xの最大値・最小値は、それぞれ振幅のA、−Aということになります。

さて、今回の単振動の位置に関する知識をしっかり覚えて欲しいのですが、注意してほしいことがあります。それは単振動の位置x=Asinωtという式はすべての単振動に当てはまる式ではないということです。この式はあくまでも基本形で、単振動がはじめ下向きの運動であれば −Asinωt になります。またsinではなく、cosを使う場合なども出てきます。

単振動の位置x=Asinωtの式が基本形であることに注意して、練習問題を解いていきましょう。