2つの点電荷による電気力線、等電位面を作図する問題ですね。

電気力線は電場の方向に沿った線 でしたね。 プラスの電荷から放射状に吐き出され、マイナスの電荷に吸い込まれるような電気力線 を描きましょう。

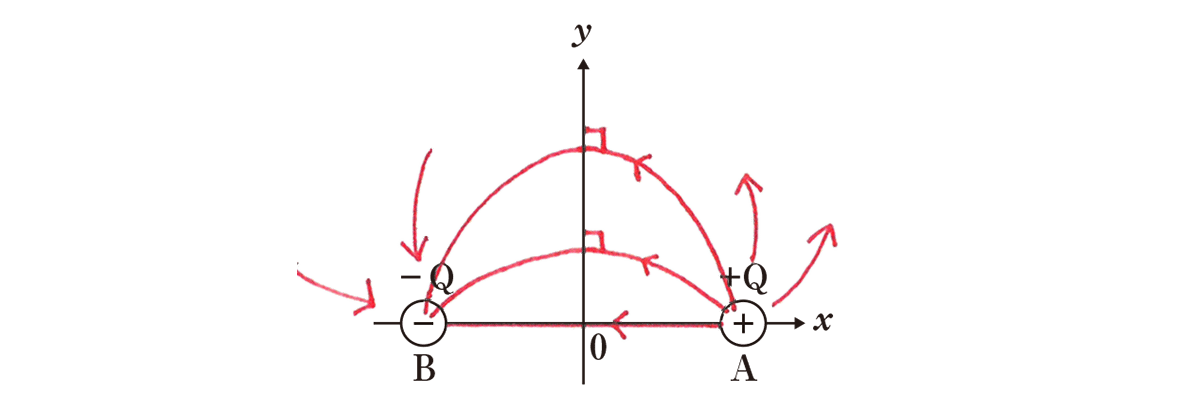
このとき重要になるのが、 電気力線はy軸と垂直に交わるように描く という点です。なぜかわかりますか？試しに、y軸上に1つ点を取り、Cとしてみましょう。

点Aによる電場は遠ざかる方向に大きさE_A、点Bによる電場は近づく方向に大きさE_Bとなります。このときE_A=E_Bですね。点A、Bの点電荷の電気量の絶対値がQで等しく、点A,Bから点Cまでの距離も等しいので、点Cでの合成電場は図のようにx軸と平行になります。

y軸上の点は、合成電場の方向がx軸に平行 なので、電気力線はy軸と垂直に交わるのですね。

y≧0での等電位面を考えます。 等電位面は電気力線と垂直に交わる という性質がありましたよね。

等電位面は電気力線と垂直に交わっているということを強調して描いてください。

また、(1)と同様、y軸上の点にはある特徴があります。y軸上の任意の点Cにおける合成電位Vを求めてみましょう。AからCまでの距離をrとすると、点Aが作る電位V_A=k(+Q)/r。点Bが作る電位V_B=k(−Q)/rとなります。
したがって、点Cでの合成電位は
V=k×(Q/r)-k×(Q/r)=0
となり、 y軸上の点はどこをとっても電位は0[V] となります。